Define Midpoint Circle Drawing Algorithm

April 07, 2022 Post a Comment

With trigonometry functions such equally sine and cosine, information technology is very piece of cake to compute for the value of x and y for any given radius and teta.

px = cx + radius * cosine(0);
py = cy + radius * sine(0);

for (teta = 1; teta <= 360; ++teta)
{
px = cx + radius * cosine(teta);
py = cy + radius * sine(teta);
line(px, py, x, y);
px = x;
py = y;
}

We've all learned this from highschool trigonometry class and it will non be tacked in this commodity. Withal, drawing a circle using these functions requires the usage of floating-indicate numbers which is ho-hum, non to mention the typecasting from floating-point to integers as plotting a pixel requires integral datatype. And finally, the large turnoff of this script is using the line segment office to connect the dots.

You can improve the higher up lawmaking by reducing the computational complexity past dividing the circle to quadrants, octants, or whatsoever.

Midpoint Circle Algorithm

Agreement the algorithm starts with the circle formula

x² + y² = r^two

For simplicity of computation, we don't take to compute for the x and y of the unabridged circle given r. We tin can split up it into quadrants, octants, or whatever suits your preference. In our case, we volition divide the circle by 8, which means we only need to compute 0 degrees to 45 degrees. Also to farther simplify, our circle will be centered at coordinates (0, 0).

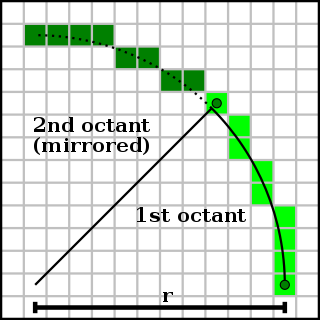
Notice on the get-go octant, that y continually increases while 10_i+1 is either on the same position as x_i or ten_i - one. We'll consider y as fast direction and ten as the slow direction in this case. This ways that x decreases past some factor of the circumvolve. Merely how do we get x based on the previous values of x and y?

For each bespeak in the circle, the following formula holds, where i is the iteration starting from 0.

x^two _i + yⁱⁱ _i = r²

To go the x we tin can rearrange the in a higher place to:

10ⁱⁱ _i = r^two - y² _i, the next indicate would exist 10² _i+one = r^two - y² _i+one

Since y is the fast direction, y increases for every iteration in the first octant, hence:

y^two _i+1 = (y_i + 1)²

Let's substitute this to x² _i+1

x² _i+1 = r² - (y_i + 1)ⁱⁱ
xⁱⁱ _i+i = rⁱⁱ - y² _i - 2y_i - 1, we can simplify by the computation past replacing rⁱⁱ - y^two _i by ten² _i, which gives us:
xⁱⁱ _i+1 = x² _i - 2y_i - ane
x_i+1 = √[ x^two _i - 2y_i - 1 ]

At present that we a formula of x that is dependent on the previous value, we can start writing our program. The following is written in C/C++ and SDL (actually all other programs below are written using the same language and framework):

void drawCircle1(SDL_Surface* surface, Sint32 cx, Sint32 cy, Uint32 r, Uint32 rgba)
{
Sint32 ten, x2, xn, y, xsurface, ysurface;

// Heart position the arrow
Uint32* pixels = (Uint32*)surface->pixels + cx + (cy * surface->w);

// Starts plotting (0, 0)
x2 = r * r;
x = sqrt(x2);
y = 0;

while (10 > y)
{
xn = (x2 - (2 * y) - 1);
x = sqrt(x2);
xsurface = x * surface->westward;
ysurface = y * surface->westward;

// First Octant
*(pixels + 10 - (ysurface)) = rgba;

// The rest of the octants
*(pixels + y - (xsurface)) = rgba;
*(pixels - y - (xsurface)) = rgba;
*(pixels - ten - (ysurface)) = rgba;
*(pixels + 10 + (ysurface)) = rgba;
*(pixels + y + (xsurface)) = rgba;
*(pixels - y + (xsurface)) = rgba;
*(pixels - x + (ysurface)) = rgba;

x2 = xn;
++y;
}
}

Output:

Information technology is of import to take note that the upper left coordinates of the screen is (0, 0), and ten and y increase as we movement southeastwards, therefore adjustments are fabricated to plot the first octant in the cartesian aeroplane. The rest of the octants are computed appropriately.

Although the above script works, it could have been more elegant if floating-betoken computation such as foursquare root, and typecasting have been eliminated.

Bresenham's Derivation of Drawing a Circumvolve

To completely remove the floating-point computation, we demand to start with the so-called Radius Error (RE). RE is can exist thought of as a difference of computation of points. If nosotros've detected a difference then we need to practice correction in x position (assuming we're working on the kickoff octant). If we're starting again with the first octant at (r, 0), we can say that RE_i, where i = 0, is zero (0), because nosotros're sure that ten = r and y = 0 at this betoken, and we can plot these two values using integral data blazon, hence we can write:

RE(ten_i, y_i) = | x^two _i + y^two _i - r² | = 0, where | | denotes absolute value.

when i = 0, on beginning octant,

RE(ten_i, y_i) = | 10^two _i + 0 - r² | = 0

Just like the Midpoint algorithm, and since we're starting with the first octant, we know that y is the fast direction and x is the slower. Therefore, as y increments, x can either stay in the same position or decrement by one (1). To requite a solution to this, nosotros ascertain a conclusion statement to determine if we demand to retain the value of x or decrement the value of x equally y increases.

RE(x_i- 1, y_i+ 1) < RE(x_i, y_i+ 1), if the value of the left manus side is less than the right, and so nosotros plot RE(ten_i- 1, y_i+ 1), otherwise RE(10_i, y_i+ 1).

To start the determination, let's substitute the value of RE. This gives united states the following equation:

= | (x_i - 1)^two + (y_i+ 1)² - r² | < | x_i ² + (y_i + 1)² - r² |

Expanding the equation gives u.s.a.

= | (10^two _i - 2x_i + 1) + (y^two _i+ 2y_i + 1) - r^two | < | x_i ^two + (y² _i + 2y_i + 1) - r² |

Rearranging volition give us

= | xⁱⁱ _i - 2x_i + i + y^two _i+ 2y_i + ane - r^two | < | x_i ² + y² _i + 2y_i + i - r² |
= | ten² _i + y² _i- r²+ 2y_i + 1 + 1 - 2x_i | < | x_i ² + y² _i - r²+ 2y_i + i |
= | (x² _i + y^two _i- r²+ 2y_i + 1) + (one - 2x_i) | < | (ten_i ⁱⁱ + y² _i - r²+ 2y_i + 1) |

Since absolute function | | requires additional library, we replace it by squaring both sides of the equation.

= [ (10^two _i + y² _i- r²+ 2y_i + i) + (1 - 2x_i) ]² < [ (x_i ² + yⁱⁱ _i - r²+ 2y_i + 1) ]ⁱⁱ

Expanding the left hand side of the equation gives us:

= (x^two _i + y^two _i- r²+ 2y_i + ane)² + two(1 - 2x_i)(x² _i + yⁱⁱ _i- r^two+ 2y_i + 1) + (1 - 2x_i)²
< (x_i ² + y² _i - rⁱⁱ+ 2y_i + 1)²

Canceling out (ten_i ^two + y² _i - r²+ 2y_i + 1)²

= 2(one - 2x_i)(x^two _i + y² _i- r^two+ 2y_i + 1) + (1 - 2x_i)ⁱⁱ < 0

And since we know that x > 0 in the first octant, the term (ane - 2x_i) < 0, dividing both sides volition cancel out the negative, giving usa

(a) = 2 [ xⁱⁱ _i + y² _i- r²+ 2y_i + 1 ]+ (i - 2x_i) > 0
(b) or simply = 2 [ RE (ten_i, y_i) + Y_change] + X_change > 0

If the argument is true, and so we decrement the value of 10, otherwise, x stays at the same position.

Consider statement (a), to translate the decision statement to program, we write:

void drawCircle2(SDL_Surface* surface, Sint32 cx, Sint32 cy, Sint32 r, Uint32 rgba)
{
Sint32 x, x2, xn, y, y2, r2, re, xsurface, ysurface;

// Center position the pointer

Uint32* pixels = (Uint32*)surface->pixels + cx + (cy * surface->w);
r2 = r * r;
10 = r;
x2 = x * x;
y = 0;

while (x > y)
{
xsurface = ten * surface->west;
ysurface = y * surface->due west;

y2 = y * y;
re = x2 + y2 - r2;

if ((two * re) + (4 * y + 2) + (1 - (two * ten)) > 0)
{
--x;
x2 = x * x;
}

// Outset Octant
*(pixels + x - (ysurface)) = rgba;

// The rest of the octants
*(pixels + y - (xsurface)) = rgba;
*(pixels - y - (xsurface)) = rgba;
*(pixels - x - (ysurface)) = rgba;
*(pixels + x + (ysurface)) = rgba;
*(pixels + y + (xsurface)) = rgba;
*(pixels - y + (xsurface)) = rgba;
*(pixels - x + (ysurface)) = rgba;

++y;
}
}

The in a higher place script tin notwithstanding be further improved past eliminating multiplication in the script by the post-obit:

bit shifting to the left one fourth dimension multiplies the integer by 2, flake shifting to the left ii times multiples the integer past 4 (refer to drawCircle3() function in attached .cpp file)
Consider the iii quantities in the equation at close inspection and determine their values at dissimilar values of ten_i and y_i. Let's find a way to do it iteratively to reduce the computational complexity (removal of squares - multiplication).
- RE (x_i, y_i) = x² _i + y² _i- r²
- Y_change= 2y_i + 1
- X_change= ane - 2x_i
Since we're starting with x =r, y = 0, and RE (x₀, y₀) = 0, let's set RE initially to 0, Y_change = ane, and X_alter = i - (2 * r);
We increase RE byY_change every iteration since, y is in the fast direction.
We increment Y_change by 2 based on the formula.
We compare ( two x RE + Xchange > 0), if truthful then that's the fourth dimension nosotros decrement ten and increment RE by X_change and increment X_change y 2 based on the formula.

The consummate program of plotting a circumvolve using integer arithmetic is shown beneath:

void drawCircle4(SDL_Surface* surface, Sint32 cx, Sint32 cy, Sint32 r, Uint32 rgba)
{
Sint32 ten, y, xsurface, ysurface;
Sint32 xchange, ychange, re;

// Center position the pointer
Uint32* pixels = (Uint32*)surface->pixels + cx + (cy * surface->w);

x = r;
y = 0;
xsurface = x * surface->w;
ysurface = y * surface->w;

xchange = 1 - (r << one);
ychange = 1;
re = 0;

while (x > y)
{
// First Octant
*(pixels + 10 - (ysurface)) = rgba;

// The rest of the octants
*(pixels + y - (xsurface)) = rgba;
*(pixels - y - (xsurface)) = rgba;
*(pixels - ten - (ysurface)) = rgba;
*(pixels + x + (ysurface)) = rgba;
*(pixels + y + (xsurface)) = rgba;
*(pixels - y + (xsurface)) = rgba;
*(pixels - 10 + (ysurface)) = rgba;

++y;
re += ychange;
ychange += ii;
if ((re << 1) + xchange > 0)
{
--x;
xsurface -= surface->w;
re += xchange;
xchange += 2;
}
ysurface += surface->w;
}
}

And so there you become, an elegant solution (with an explanation of the derivation) as to how you tin can draw a circle efficiently. Experience free to play around with the codes and import it to your programming language of choice.

shaffereverchist.blogspot.com

Source: https://www.everettgaius.com/article/how-draw-circle-midpoint-and-bresenhams-algorithm